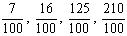PORCENTAGEM

PORCENTAGEM

    Razão centesimal 

    Toda a razão que tem para consequente o número 100 denomina-se razão centesimal. Alguns exemplos:

    Podemos representar uma razão centesimal de outras formas:

    

    As expressões 7%, 16% e 125% são chamadas taxas centesimais ou taxas percentuais.

    Considere o seguinte problema:

    João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu?    Para solucionar esse problema devemos aplicar a taxa percentual (50%) sobre o total de cavalos.

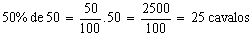
    Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada.

    Portanto, chegamos a seguinte definição:

Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor.

    Exemplos:

• Calcular 10% de 300.        
     
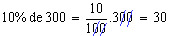
• Calcular 25% de 200kg.
          
  
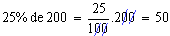
  Logo, 50kg é o valor correspondente à porcentagem procurada.
  

    EXERCÍCIOS:

    1) Um jogador de futebol, ao longo de um campeonato, cobrou 75 faltas, transformando em gols 8% dessas faltas. Quantos gols de falta esse jogador fez?

    

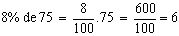
    Portanto o jogador fez 6 gols de falta.

    2) Se eu comprei uma ação de um clube por R$250,00 e a revendi por R$300,00, qual a taxa percentual de lucro obtida?

    Montamos uma equação, onde somando os R$250,00 iniciais com a porcentagem que aumentou em relação a esses R$250,00, resulte nos R$300,00.

    

    Portanto, a taxa percentual de lucro foi de 20%.

EXERCÍCIOS 

1) Quanto é 15% de 80?

Aulas de Porcentagem em Vídeo

2) Quanto é 70% de 30?

3) Quanto é 150% de 45?

4) Quanto é 100% de 40?

5) Expresse a razão de 19 para 25 como uma porcentagem.

6) 30% da população de uma cidade litorânea mora na área insular e os demais 337.799 habitantes moram na área continental. Quantas pessoas moram na ilha?

7) Se 4% de um número é igual a 15, quanto é 20% deste número?

8) Do meu salário R$ 1.200,00 tive um desconto total de R$ 240,00. Este desconto equivale a quantos por cento do meu salário?

9) Eu tenho 20 anos. Meu irmão tem 12 anos. A idade dele é quantos por cento da minha?

10) Meu carro alcança uma velocidade máxima de 160 km/h. O carro de meu pai atinge até 200 km/h. A velocidade máxima do carro do meu pai é quantos por cento da velocidade máxima do meu carro?

11) Por um descuido meu, perdi R$ 336,00 dos R$ 1.200,00 que eu tinha em meu bolso. Quantos por cento eu perdi desta quantia?

12) Dei ao meu irmão 25 das 40 bolinhas de gude que eu possuía. Quantos por cento das minhas bolinhas de gude eu dei a ele? Com quantos por cento eu fiquei?

Iniciando o ano com matérias que irão cair na prova da polícia militar do Espírito Santo

REGRA DE TRÊS SIMPLES E COMPOSTA

Regra de Três Simples

O problema que envolve somente duas grandezas  diretamente é mais comumente chamado de regra de três simples. 

Exercício de fixação da definição: 

Um automóvel percorre um espaço de 480 Km em 02 horas. Quantos kms ele percorrerá em 06 horas? 

Grandeza 1: Distância percorrida

Grandeza 2: Tempo necessário 

Cálculo:

Distância 1  =  480 Km - 02 horas

Distância 2  =   ?   Km - 06 horas 

01 hora percorrida = 240 km

06 horas percorrida = 240 Km x 6

Resultado: 1440 Kms

Método mais prático de solução da regra de três simples

Faça um X  na equação, pegue o primeiro número de cima (480) e multiplique pelo segundo número de baixo (06) depois é só dividir pelo número que restou (02) - O que você deseja saber está em Km, portanto a resposta será em Km

480 km - 02 horas

            X

  ?   km - 06 horas 

Resp: ? = 480 . 06 / 02 = 1440 Km

Regra de três composta

Este tipo de cálculo de regra de três envolve mais de duas grandezas proporcionais. 

Exercícios de fixação da definição: 

1) Se 20 homens trabalhando durante 15 dias constroem 500 metros de um muro, quantos homens serão necessários para construir mais 1000 metros deste muro em 30 dias? 

Grandeza 1 : Número de homens trabalhando

Grandeza 2 : Tempo de duração do trabalho

Grandeza 3 : Tamanho do muro 

2) Se 10 carros consomem  em 05 dias a quantidade de 1000 litros de gasolina, quantos carros usaremos  para consumir somente 500 litros de gasolina no espaço de  02 dias?? 

Grandeza 1: Número de carros

Grandeza 2: Número de dias

Grandeza 3: Quantidade combustível 

Método mais prático de solução da regra de três composta 

Faça a comparação da grandeza que irá determinar com as demais grandezas. Se esta grandeza for inversa, invertemos os dados dessa grandeza das demais grandezas. 

A grandeza a se determinar não se altera, então, igualamos a razão das grandezas e determinamos o valor que se procura. 

Veja: 

1) Na alimentação de 02 bois, durante 08 dias, são consumidos 2420 kgs de ração. Se  mais 02 bois são comprados, quantos quilos de ração serão necessários para alimentá-los durante 12 dias.

Assim: serão necessários 7260 Kgs de ração

2) Se 10 metros de um tecido custam R$ 50,00, quanto custará 22 metros ?

Solução: O problema envolve duas grandezas (quantidade de tecidos e preço da compra) 

          

Assim: 22 metros custarão R$ 110,00 

3) Em 06 dias de trabalho, 12 confeiteiros fazem 960 tortas. Em quantos dias 04 confeiteiros poderão fazer 320 tortas 

Solução: O problema envolve três grandezas (tempo, número de confeiteiros, quantidade de tortas) 

Exercícios de regra de três simples e composta

As respostas estão no final da página.

01 – Com 10 kg de trigo podemos fabricar 7kg de farinha. Quantos quilogramas de trigo são necessários para fabricar 28 kg de farinha? 

02 – Com 50 kg de milho, obtemos 35 kg de fubá. Quantas sacas de 60 kg de fubá podemos obter com 1 200 kg de milho ? 

03 – Sete litros de leite dão 1,5 quilos de manteiga. Quantos litros de leite serão necessários para se obterem 9 quilos de manteiga ? 

04 – Em um banco, contatou-se que um caixa leva, em média, 5 minutos para atender 3 clientes. Qual é o tempo que esse caixa vai levar para atender 36 clientes ? 

05 – Paguei R$ 6,00 por 1.250 kg de uma substância. Quanto pagaria por 0,750 kg dessa mesma substância ? 

06 – Seis máquinas escavam um túnel em 2 dias. Quantas máquinas idênticas serão necessárias para escavar esse túnel em um dia e meio ?  

07 – Uma fonte fornece 39 litros de água em 5 minutos. Quantos litros fornecerá em uma hora e meia ? 

08 – Abrimos 32 caixas e encontramos 160 bombons. Quantas caixas iguais necessitamos para obter 385 bombons ? 

09 – Um automóvel percorre 380 km em 5 horas. Quantos quilômetros percorrerá em 7 horas, mantendo a mesma velocidade média ?

10 – Um automóvel gasta 24 litros de gasolina para percorrer 192 km. Quantos litros de gasolina gastará para percorrer 120 km ? 

Vídeo de Surf

2009 left over Clips from Tom Jennings on Vimeo.

para quem faz cálculos errados.....rsrsr

SÓLIDOS DE PLATÃO

Ao que se sabe o primeiro contato de Platão com os sólidos, poliedros regulares, terá sido provocado por Arquitas, em Itália. Para Platão, o Universo era formado por um corpo e uma alma ou inteligência.
Platão concebia o mundo como sendo constituído por quatro elementos básicos: a Terra, o Fogo, o Ar e a Água, e estabelecia uma associação mística entre estes e os sólidos. Na matéria havia porções limitadas por triângulos ou quadrados, formando-se elementos que diferem entre si pela natureza da forma das suas superfícies periféricas. Se forem quadradas temos o cubo, ao qual Platão fazia corresponder a Terra. No caso de serem triângulos, formando um tetraedro, associa-se ao Fogo, cuja natureza penetrante está simbolizada na agudeza dos seus vértices. O octaedro foi associado ao Ar e o icosaedro à Água. O quinto sólido, o dodecaedro, foi considerado por Platão como o símbolo do Universo.
Embora designados como sólidos platónicos (apesar de alguns autores os designarem por Corpos Cósmicos), Proclus atribui a construção destes poliedros a Pitágoras, supondo-se que é também a este que se deve o teorema: "Há somente cinco poliedros regulares".
TETRAEDROEste poliedro é formado por quatro triângulos equiláteros. E em cada um dos vértices encontra-se o mesmo número de lados (arestas). O prefixo tetra deriva do grego e significa quatro (quatro faces).

HEXAEDROO cubo é o único poliedro regular com faces quadrangulares. Cada vértice une três quadrados. O cubo tem 6 faces, pelo que também se pode chamar de hexaedro (hesa significa seis em grego).

OCTAEDROAs faces deste poliedro são também triângulos equiláteros, mas em cada vértice reúnem-se quatro triângulos. Assim, o total das faces é oito, pelo que o poliedro se chama octaedro (octa significa oito em grego).

DODECAEDROO dodecaedro é o único poliedro regular cujas faces são pentágonos regulares. Em cada vértice encontram-se três pentágonos. Assim, este poliedro é formado por doze faces e daí ter o nome de dodecaedro (dodeca significa doze em grego).

ICOSAEDRONeste poliedro são cinco os triângulos equiláteros que se encontram em cada vértice, perfazendo vinte faces. Por isso, o poliedro se chama icosaedro (icosa significa 20 em grego).

Os poliedros regulares (os sólidos anteriores) verificam a relação de Euler:

N.º faces + N.º vértices = N.º arestas + 2. F + V = A + 2
Planificações:
Se quiser saber mais, consulte os seguintes links:
http://pt.wikipedia.org/wiki/Poliedrohttp://maccsg1.macc.unican.es/pcorc/platonicos.html

Não deixe os números te derrubarem

Saindo do mar em mais um dia de boas ondas.